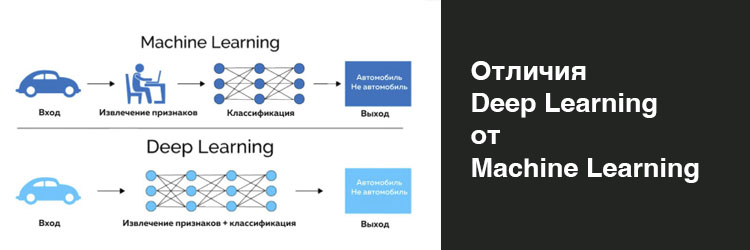
Урок 2.8. Понятие Deep Learning и Machine Learning, в чем отличие
Как известно, нейронные сети – это некий математический аппарат, который получает на вход значения и преобразует их в соответствии с правилами, которые были заложены в него. Нейронные сети можно представить как набор нейронов, через которые проходит наш входной сигнал.
После прохождения входного сигнала через слои нейронов мы получаем выходной сигнал, который можем тем или иным способом интерпретировать.
Что же происходит с нашими данными во время их прохождения через слои сети? Ответ очень простой – к ним применяются математические преобразования: считается взвешенная сумма на входе в нейрон, к ней добавляется коэффициент смещения. В самом же нейроне полученное значение обрабатывается функцией активации. Давайте разберемся поподробнее: что же такое функция активации, рассмотрим виды функций и попытаемся разобраться - какую же из них выбрать.
Проводя аналогии с биологическими нейронными сетями в наиболее простой форме, то функцию активации можно представить как ступенчатую функцию, нейрон может либо возбудиться, либо нет. Для такой активационной функции мы можем использовать следующую математическую формулу:
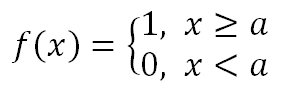
где а – пороговый параметр
Выглядеть такая функция будет следующим образом:
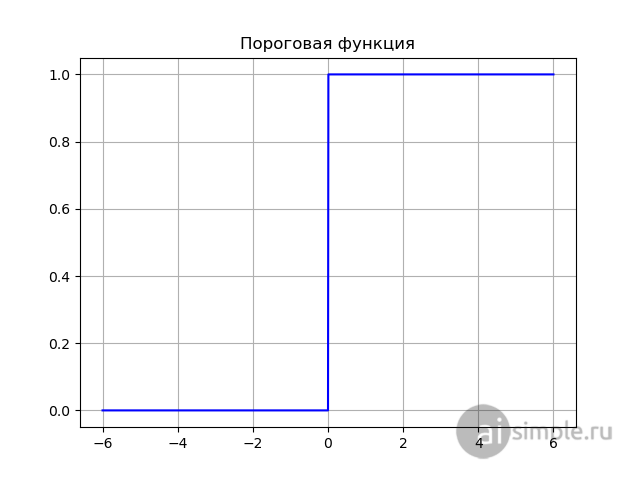
Пороговая функция активации является наиболее простой из функций, однако обладает большим количеством недостатков. Например, в задачах классификации, мы зачастую оперируем понятиями нечеткой логики и не можем утверждать, что исследуемый нами пример принадлежит к тому или иному классу на 100%, однако, при использовании пороговой функции, мы можем получать только 2 варианта: 100% и 0%, что не подходит для задач множественной классификации, поскольку существует вероятность, что 2 нейрона превысят пороговое значение. Поэтому можно смело отказываться от использования пороговой функции для обучения своей нейронной сети.
Следующая простейшая математическая кривая, которая приходит в голову – это линейная функция:
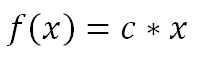где с - коэффициент пропорциональности
Вид линейной функции с коэффициентом с = 2: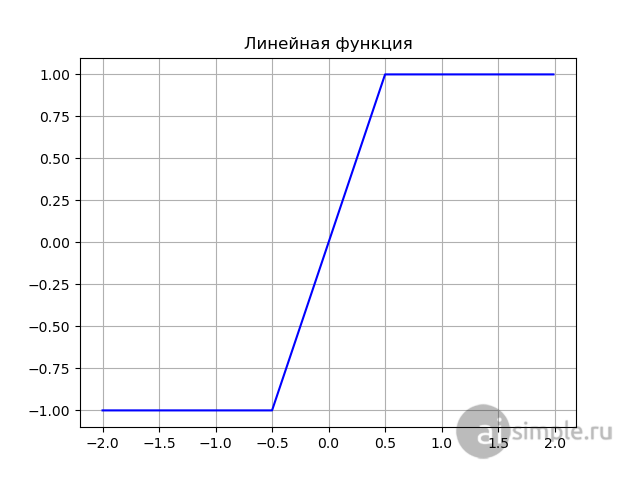
Линейная функция выглядит сложнее, чем пороговая, но ее линейная природа портит всю картину обучения. Во-первых, как известно, для обучения нейронной сети используется метод обратного распространения ошибки, который подразумевает под собой использование производной для функции активации, вспоминая курс высшей математики, можно смело утверждать, что ее производная будет равна коэффициенту пропорциональности C. Если углубиться в процесс обучения нейронных сетей, то становится понятно, что градиент является тем самым “двигателем” наших весовых коэффициентов, а если он постоянен и не зависит от изменения входных значений.
Во-вторых, как сказано выше – нейронная сеть является математическим аппаратом, значит - ее можно описать математическими операциями, линейная природа функции приводит к тому, что многослойный перцептрон становится эквивалентным однослойному.
Как стало ясно выше, использование линейных функций не удовлетворяет наши задачи, поэтому рассмотрим несколько нелинейных активационных функций, которые наиболее часто используются при обучении.
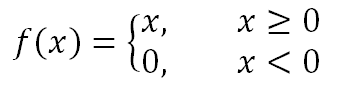
ReLU - нелинейная функция и любую другую функцию можно аппроксимировать комбинацией ReLU.
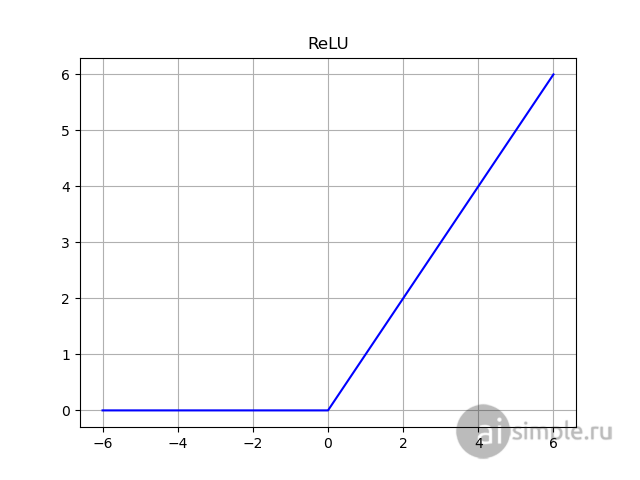
В чем же преимущество ReLU? Самый главный плюс это ее математический вид, функция требует меньше вычислительных ресурсов, что ускоряет физическое время обучения нейронной сети, это хорошо подходит для создания глубинных нейронных сетей. Также, используя ReLU, мы можем инактивировать некоторые нейроны, это опять же сделает нашу нейросеть более быстрой в пересчете времени на одну эпоху обучения.
Но, как и у любой функции. у ReLU существуют недостатки, это связано с тем, что отрицательные входные значения дадут на выходе нулевой градиент, что негативно скажется на процессе обучения нейронной сети из-за отсутствия обновления весовых коэффициентов. Эта проблема частично решается модификацией ReLU, в которой при отрицательных значениях входного параметра присваивается некая линейная функция с маленьким коэффициентом пропорциональности, что позволяет избавиться от нулевого градиента и в процессе обучения корректировать веса.
Пожалуй, наиболее популярная функция активационная функция – это сигмоидная логистическая функция.
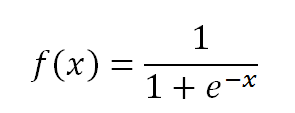
Сигмоида очень часто применяется в задачах классификации, поскольку она является гладкой функцией и меняется в диапазоне от -1 до 1.
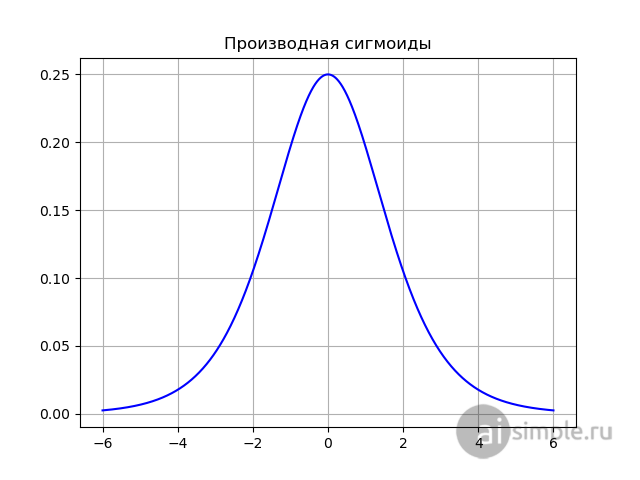
Еще одним достоинством логистической функции является вид ее производной производной. При вычислении производной мы используем те значения, которые мы получили на предыдущем шаге, что экономит время за счет упрощения математических операций:
Как видно из графика, представленного ниже, производная имеет наибольшее значение в промежутке [-2; 2], что позволяет входным значениям быстрее прижиматься к границам диапазона значений, иными словами, быстрее определять насколько активен нейрон. Однако, приближение значений функции активации к границам, опять же, приводит к затуханию градиента, и как следствие, почти не обновляемым весовым коэффициентам.
Несмотря на грозное название, за этим монстром скрывается лишь модифицированная сигмоида:
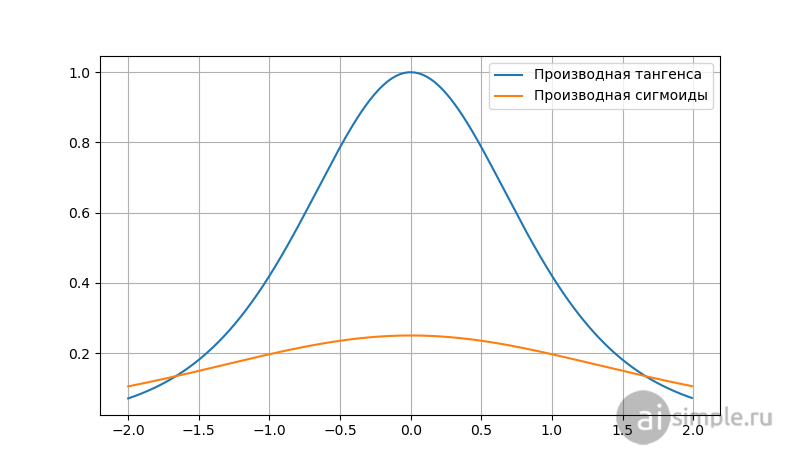
Поэтому, можно смело сказать, что все преимущества и недостатки сигмоиды в равной степени относятся и к тангенсу. Различия проявляются лишь в градиенте тангенциальной функции, он выше, это видно из сравнения производных на графике ниже.
Помимо формул, представленных выше, существуют множество других функций активации, исследователи в области искусственного интелекта постоянно ищут новые способы улучшить нейронные сети, в том числе модифицируя уже существующие способы и приемы обработки входных сигналов. Выбор активационной функции одна из первоочередных задач для построения правильной нейронной сети, однако, не существует единого правила, в каком случае какую из функций применять. Есть лишь практика, которая показывает, что ReLU лучше показывает себя как аппроксиматор, а сигмоида и гиперболический тангенс чаще используются в задачах классификации.
При решении сложных задач с использованием многослойных сетей возможно комбинировать функции на разных слоях, чтобы добиться наиболее высокой точности и скорости обучения.
