Оценка последствий химических аварий на опасных производственных объектах с использованием нейросетей

 

В статье рассматривается возможность использования ячеечно-нейросетевых моделей для оценки последствий загрязнения воздуха в результате аварии на опасном производственном объекте. Изложены отличия ячеечно-нейросетевых моделей от традиционно используемых для решения аналогичных задач, показаны их преимущества. Приведены результаты и выполнен их сравнительный анализ для ячеечно-нейросетевых моделей с различными типами ячеек и способами учёта изменений во внешней среде.

В современном индустриальном обществе проблемам экологической и промышленной безопасности уделяется повышенное внимание. С одной стороны, растущие потребности человечества требуют увеличения объемов производства. С другой стороны, это неминуемо приводит к увеличению нагрузки на экологические системы вследствие увеличения объемов выбросов загрязняющих веществ при нормальном функционировании производств и как результат возникающих аварийных ситуаций. В связи с этим в научном сообществе значительное внимание уделяется разработке новых, современных методов решения таких задач, как прогнозирование загрязнения атмосферы, идентификация его источников и других.

Традиционно для их решения используются математические модели и методики оценки последствий загрязнения атмосферного воздуха, основанные на сложных системах дифференциальных уравнений, описывающих динамику распространения примесей. Вместе с этим математическое описание данных процессов предельно затруднено вследствие высокой значимости влияния дополнительных факторов: рельефа местности, метеоусловий и других. Серьезным ограничением используемых моделей и методик является невозможность или неполнота учета этих факторов в процессе длительного и многокилометрового рассеяния примесей, в связи с чем в них принято допущение о постоянстве метеорологических и других характеристик, что в большинстве случаев противоречит реально наблюдаемой картине. Данное допущение обусловливает ориентацию используемых расчетных методик на наихудшие значения и комбинации факторов, влияющих на распространение примеси загрязняющего вещества. Тем самым реально имеющие место в результате загрязнения экологические последствия необоснованно завышаются. Наличие недостатков и ограничений существующей методической базы для решения задач экологической безопасности подтверждается современными исследованиями, отраженными, например, в работах [1, 2].

В настоящее время для математического моделирования описываемых процессов широко используются искусственные нейронные сети, клеточные автоматы и другие методы, позволяющие эффективно решать вышеуказанные задачи экологической и промышленной безопасности, снимая при этом многие ограничения. Анализ ряда печатных работ [3, 4] показал, что искусственные нейронные сети позволяют значительно проще получить сопоставимые по точности результаты, чем расчётные методики, а также дают возможность усложнить задачу за счёт оперативного учёта изменений внешней среды.

В данной статье показаны результаты практического применения различных видов ячеечно-нейросетевых моделей для решения задачи оценки последствий загрязнения атмосферы в результате аварийного выброса на промышленном объекте.

Рассмотрим особенности ячеечно-нейросетевых моделей применительно к решаемым задачам. Идея ячеечно-нейросетевых моделей берет начало от классических ячеечных моделей, которые нашли широкое применение при решении задач химии и химической технологии. Их эффективность высока при математическом описании неидеальных потоков в реакторах различных типов. Они предусматривают разделение изучаемого пространства на одинаковые по размеру ячейки, в которых состояние среды однородно по свойствам, и математическое описание изменения состояния среды от ячейки к ячейке.

Основные принципы ячеечных моделей были использованы при разработке ячеечно-нейросетевых моделей, предназначенных для решения задач экологической безопасности химических производств. Основными отличительными особенностями разработанных моделей являются:

– невозможность ограничения предельных размеров пространства распространения примеси загрязняющего вещества;

– использование для описания изменения состояния ячеек моделей на основе искусственных нейронных сетей.

Первая особенность приводит к невозможности использования конечного количества ячеек как характеристического параметра модели. Вместо этого предложено устанавливать фиксированный размер ячейки и её форму. Анализ состояния ячеек продолжается до тех пор, пока соответствующие характеристики изменяются значимо для решаемой задачи. Вторая особенность позволяет снять проблему невозможности решения системы линейных дифференциальных уравнений классической ячеечной модели, связанную с отсутствием физических границ распространения примеси, а также получить более точное математическое описание изменения состояния ячеек, позволяющее учесть множество дополнительных параметров и неопределённостей, связанных с условиями внешней среды (рельефом местности, метеоусловиями и их изменением во времени).

Основные теоретические положения ячеечно-нейросетевого моделирования изложены в работе [5]. Основываясь на них, сформулируем общую постановку задачи ячеечно-нейросетевого моделирования на примере оценки экологических последствий аварийного выброса опасного химического вещества и его распространения в атмосферном воздухе на территории, прилегающей к химическому производству.

Объект моделирования – примесь загрязняющего вещества, присутствующая в воздухе в результате аварийного выброса, и её поведение (изменение концентрации) во времени и пространстве. Цель моделирования – возможность оценки концентрации примеси, продолжительности негативного воздействия на окружающую среду, в том числе живые организмы и человека, и размеров территории, подвергшейся негативному воздействию.

В соответствии с концепцией, заложенной в ячеечные модели, концентрация загрязняющего вещества в любой точке одной ячейки в один и тот же момент времени одинакова. Концентрации в различных ячейках в один и тот же момент времени в общем случае различаются.

Принимаем, что движение среды (примеси) осуществляется от каждой ячейки к её соседям и обратно под влиянием движущих сил, обусловленных градиентом концентрации загрязняющего вещества, условиями внешней среды и другими при отсутствии внешней границы, делающей такое движение невозможным. Естественной преградой, препятствующей процессу распространения примеси, является поверхность земли.

При решении задач экологической безопасности наиболее существенное значение уделяется моделированию поведения примеси в приземном слое, где обитает абсолютное большинство организмов, которые могут пострадать в результате загрязнения воздушного бассейна, живут и работают люди. Так, замеры концентраций примесей в воздухе, оценки токсического воздействия на человека проводятся на высоте 1,5–2 м от уровня земли.

Кроме того, процессы распространения примеси в приземном слое существенно отличаются от аналогичных процессов на бо́льших расстояниях от земли ввиду ряда особенностей, связанных с поглощением небольшого количества примеси земной поверхностью, изменением направления распространения вследствие особенностей рельефа местности, атмосферной инверсии и других. Таким образом, модели распространения осложняются необходимостью дополнительного учёта факта близости к земной поверхности и ее природы.

Всё вышеперечисленное обусловливает не только возможность, но и целесообразность допущения о рассмотрении единственного (приземного) слоя пространства распространения загрязняющего вещества. При этом его высота может быть любой, в том числе и такой, на которой наиболее важно оценивать концентрации, токсодозы, размеры зон загрязнения и т. п.

Очевидно, что смоделированная концентрация примеси в любой точке ячейки тогда должна быть предельно близка по величине к реальной концентрации в точке пространства, совпадающей координатами с центром масс вершин данной ячейки на заранее оговорённой высоте, например, 2 м.

В качестве входных переменных ячеечно-нейросетевой модели могут использоваться известные состояния ячеек, метеорологические условия, а также различные другие характеристики, непосредственно влияющие на процесс распространения примеси. Выходными переменными модели являются состояния тех же самых ячеек в более поздний момент времени или состояния соседних ячеек. Параметры модели – размеры и форма ячеек, а также порядок их взаимного расположения. В работе рассмотрены квадратные ячейки с равномерным порядком и гексагональные ячейки.

Исследуется аварийный выброс газообразного аммиака массой 29 тонн. Авария развивается при следующих метеорологических параметрах: температура воздуха 20 градусов Цельсия, переменная облачность, атмосферное давление 760 мм ртутного столба, светлое время суток, местность - городская застройка.

Исходная выборка данных для обучения нейронной сети была получена на основе результатов вычислительного эксперимента по методике [6].

В ходе эксперимента были найдены значения концентрации примеси аммиака в точках, соответствующих центрам масс вершин ячеек в дискретные моменты времени с шагом 10 минут при различных метеоусловиях: скорости ветра 0,5–2,0 м/с, направлении ветра от –45° до +45°.

В соответствии с представленным далее моделями из исходной выборки были выделены входные и выходные значения. Выборка была предварительно обработана с целью исключения повторяющихся и противоречивых примеров и разделена на обучающее и тестовое множества примеров.

Особенность нормирования исходных данных в решаемых задачах заключалась в наличии малого количества примеров с очень высокими концентрациями аммиака и большого количества примеров с концентрациями от долей до нескольких единиц ПДК. В связи с этим пришлось отказаться от обычного линейного нормирования данных, которое привело бы к тому, что большинство входных и выходных значений оказались околонулевыми. Вместо этого фактические концентрации были предварительно прологарифмированы, а только затем подвергнуты линейной нормализации. При логарифмировании и обратной процедуре получения концентраций в исходных единицах измерения использовались следующие соотношения:

 

  

где C, C_н – обычная (мг/м³) и нормированная концентрации загрязняющего вещества в атмосферном воздухе;

Итоговая обучающая выборка составила 9814 примеров.

Для оценки возможности применения ячеечно-нейросетевых моделей для оценки последствий аварийных выбросов проверим соответствие результатов ячеечно-нейросетевого моделирования и моделирования на основе традиционно используемой для этой цели расчетной методики [6]. Допущения о постоянстве метеоусловий в процессе рассеяния примеси, действующие для нее, распространим в этом примере и на ячеечно-нейросетевую модель.

Для моделирования мгновенной зоны загрязнения и профиля концентрации загрязняющего вещества используем двухуровневые ячеечно-нейросетевые модели с квадратными и гексагональными ячейками (рис. 1).

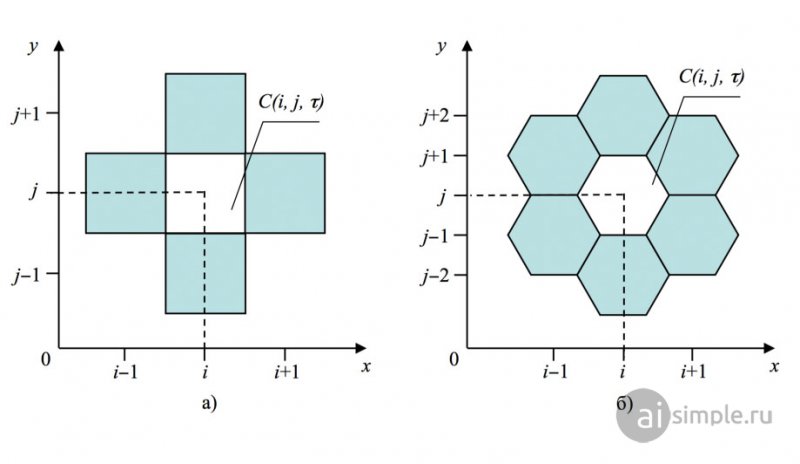Рис. 1. Графическая интерпретация ячеечно-нейросетевой модели:

а) с квадратными ячейками; б) с гексагональными ячейками (i, j – индексы ячеек по координатным осям x, y)

На рис. 2 приведен пример схемы ячеечно-нейросетевого моделирования в случае гексагональных ячеек при расчете концентрации в базовой ячейке в прогнозируемый момент времени.

 

Математически нейросетевые модели и соотношения для расчёта координат влияющих ячеек относительно базовой ячейки могут быть записаны в виде:

– для равномерно упорядоченных ячеек квадратной формы:

 

– для ячеек гексагональной формы:

 

где C[i, j] – концентрация внутри ячейки пространства с индексами i, j; X[i, j], Y[i, j] – координаты ячейки пространства по осям; d – размер грани ячейки.

Для построения мгновенной зоны загрязнения и профиля концентрации в точке также используется схема ячеечно-нейросетевого моделирования, представленная на рис. 2. Для формирования поля концентраций в группе ячеек требуется рассчитать состояние в каждой отдельно взятой ячейке, зная предшествующие концентрации во всех окружающих их соседних ячейках. При получении профилей зависимости концентраций от координаты вдоль или поперек оси направления ветра можно воспользоваться данными о состоянии лишь некоторых ячеек мгновенной зоны, расположенных вдоль соответствующих координатных осей. Для получения профилей изменения концентрации во времени для точки с фиксированными координатами на Т моментов времени вперед необходимо иметь информацию о состоянии интересующей ячейки и ячеек ее окружения Т уровней в последний момент времени.

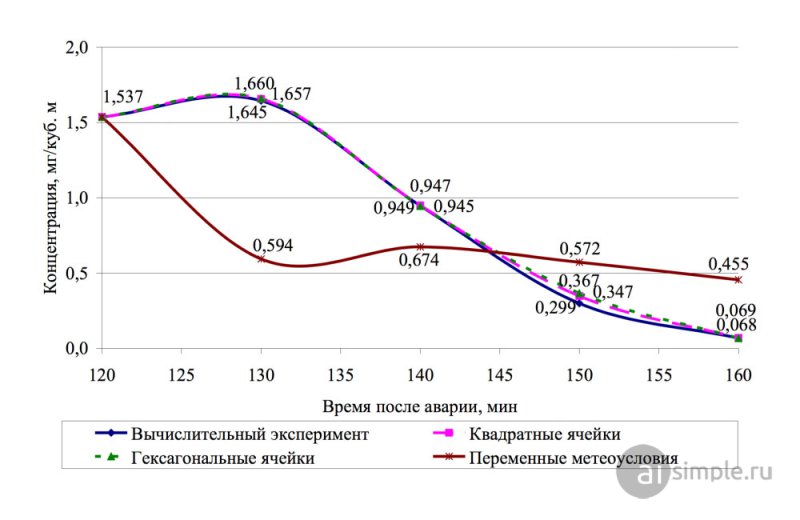Рис. 3. Изменение концентрации аммиака во времени

Полученные результаты моделирования (рис. 3) сравнивались с данными вычислительного эксперимента, полученными по методике [6] при постоянных метеоусловиях. Также проводилось сравнение результатов между ячеечно-нейросетевыми моделями с квадратными и гексагональными ячейками.

При постоянных метеоусловиях средняя абсолютная ошибка рассчитанных концентраций как для моделей с квадратными, так и с гексагональными ячейками составила около 0,02 мг/м³, что позволяет сделать выводы, во-первых, о практической идентичности полученных данных результатам компьютерного моделирования по методике [6] и, как следствие о возможности использования ячеечно-нейросетевых моделей для решения задачи прогнозирования изменения концентрации загрязняющего вещества во времени, а во-вторых, об отсутствии существенных различий в точности для моделей с различной формой ячеек. Дополнительные расчёты показали, что при снижении объема обучающей выборки примерно на порядок модели с гексагональными ячейками имеют ощутимое преимущество перед моделями с квадратными ячейками (разница в средних ошибках увеличивается в 1,5–2,5 раза).

Для учёта влияния метеорологических характеристик и их изменения на концентрацию вредной примеси в модели (3), (4) в качестве аргументов функции добавляются соответствующие переменные, например, скорость ветра, температура, влажность и другие. Внесем изменение в исходные данные рассмотренного выше примера. Пусть скорость и направление ветра в процессе рассеяния примеси изменяются в соответствии со следующим сценарием:

Время после аварии, мин	120	130	140	150	160	170
Скорость ветра, м/с	2,0	1,0	0,5	0,5	1,0	1,5
Направление ветра, град.	0	20	45	30	–20	–45

С учетом выбранного сценария изменения метеоусловий была получена соответствующая зависимость концентрации аммиака от времени после аварии по модели с гексагональными ячейками, значительно отличающаяся от такой же зависимости при постоянных скорости и направлении ветра (рис. 3).

Различный характер распространения примеси аммиака наблюдается на фрагментах рис. 4, где приведены результаты моделирования зоны загрязнения, полученные с помощью пакета программ Matlab с использованием средства Neural Network Toolbox при постоянных и переменных метеоусловиях в моменты времени 120 и 130 мин после аварии. На основе графиков (рис. 3) и изображений зон (рис. 4) можно сделать следующие наблюдения: при учете изменения направления ветра и ослаблении его скорости наблюдаются:

– смещение центра облака загрязняющего вещества относительно оси постоянного направления ветра;

– уменьшение расстояния, на которое перемещается облако;

– замедление рассеяния примеси, в результате чего при выбранном сценарии изменения метеоусловий к моменту времени 160 мин не происходит падение концентрации аммиака ниже уровня максимальной разовой предельно допустимой концентрации (0,2 мг/м³), в отличие от постоянных метеоусловий.

Все вышеперечисленные наблюдения объясняются реальными физическими процессами, происходящими при рассеянии примеси в условиях изменяющейся внешней среды и подтверждают необходимость учета изменяющихся внешних факторов.

Учет изменяющихся метеоусловий в процессе длительного распространения примеси загрязняющего вещества на большие расстояния позволяет:

• точнее рассчитывать продолжительность и уровень негативного токсического воздействия;
• точнее определять размеры и местонахождение зон загрязнения и поражения;
• точнее оценивать возможные экологический, экономический и социальный виды ущербов от воздействия поражающих факторов, возникших в результате химической аварии;
• своевременно принимать наиболее правильные решения по ликвидации последствий аварий, предупреждению негативных воздействий на население и персонал, при этом наиболее эффективно и рационально используются соответствующие ресурсы.

Последующие исследования в области ячеечно-нейросетевого моделирования в задачах экологической и промышленной безопасности связаны с изучением:

– особенностей применения различных архитектур нейронных сетей для описания изменения состояния среды;

– возможности описания протекания различных процессов в трехмерном пространстве;

– экстраполирующей способности моделей во времени и пространстве;

– многосвязных моделей, прогнозирующих состояние среды одновременно в нескольких соседних ячейках и на несколько последовательных моментов времени;

– моделей с различной временной глубиной пространства входных переменных.

В области решения задач экологической безопасности планируется уделить внимание применению метода ячеечно-нейросетевого моделирования:

– для оценки последствий загрязнения воздуха постоянно действующими промышленными источниками при изменяющихся метеоусловиях;

– при исследовании процесса рассеяния примеси на территории с неоднородным типом подстилающей поверхности;

– в системах поддержки принятия решений по управлению безопасностью промышленных производств и экологической безопасностью на территории городов – промышленных центров.

Разработанные метод ячеечно-нейросетевого моделирования и ячеечно-нейросетевые модели оценки последствий загрязнения воздуха в результате аварийных выбросов планируется реализовать в информационно-моделирующей системе, которая будет использоваться для решения прикладных задач экологической безопасности и предназначена для учебных целей и проведения научных исследований, а также может быть востребована, экологическими службами промышленных предприятий, территориальными организациями, специализирующимися в области экологической экспертизы и контроля и другими.

Авторы:

Литература:

1. Губин С. А. Верификация методик для оценки последствий химических аварий/ С. А. Губин, И. В. Маклашова, С. М. Лыков, В. И. Сидоров, А. С. Печеркин, С. И. Сумской. – Химическая промышленность, 1999, № 10. – с. 58–66.
2. Крайников В. А. Понятие «энтропия» и оценка количества информации, содержащейся в ОНД-86/ В. А. Крайников, И. И. Полосин. – Экология и промышленность России, 2004, № 1. – с. 35–36.
3. Савицкая Т. В. Использование искусственных нейронных сетей для прогнозирования загрязнения атмосферного воздуха аварийными источниками при изменяющихся метеоусловиях/ Т. В. Савицкая, С. П. Дударов, С. А. Лёвушкина, А. Ф. Егоров, А. С. Лёвушкин. – Экологические системы и приборы, 2007, № 10. – с. 45–50.
4. Дударов С. П. Оценка последствий аварийного загрязнения воздуха с использованием программных средств нейросетевого моделирования/ С. П. Дударов, А. С. Лёвушкин. – Безопасность в техносфере, 2010, № 1. – с. 7–11.
5. Дударов С. П. Ячеечно-нейросетевые модели в задачах экологической безопасности/ С. П. Дударов, П. Л. Папаев, А. Н. Кудряшов, Ю. А. Карибова. – Искусственный интеллект и принятие решений, 2011, № 2. – с. 31–39.
6. Методические указания по оценке последствий аварийных выбросов опасных веществ (РД-03-26-2007). Серия 27. Выпуск 6 / Колл.авт. – М.: Научно-технический центр по безопасности в промышленности, 2008. – 124 с.